対数の基礎と応用 日常生活から科学技術までの活用法を徹底解説

はじめに

数学の中には直感的には理解しにくいけれど、使いこなすと非常に便利なツールがいくつかあります。
高校数学で出会った「対数」を覚えていらっしゃいますか？

その中でも「対数」は非常に強力でありながら、その真価が見過ごされがちです。この記事では、対数の基礎から、日常生活や科学技術、データ分析などでの応用例までを紹介し、そのすごさに迫ります。

対数とは？

対数は簡単に言うと、「ある数が、特定の基数の累乗によっていくつになるかを示すもの」です。

例えば、次のような式がを考えます。→　 2³ = 8

これを対数で表現するとこうなります → log⁡₂8 = 3

１つめの書き方は、指数表現。２つ目は、対数表現といいます。
どちらも「2を3乗すると8になる」という関係を示しています。2通りの書き方ができるということです。

指数表現を、基数（ここでは2）と数（ここでは8）でシンプルに書き換えることができるのが対数の特徴です。

対数の歴史と背景

対数は17世紀にスコットランドの数学者ジョン・ネイピアによって考案されました。当時、天文学や航海術では、非常に複雑で大きな数値の掛け算や割り算を電卓なしで計算する必要がありました。しかし、掛け算や割り算は大変時間がかかります。これを効率化するために考え出されたのが対数です。

掛け算,割り算 → 足し算,引き算に変換することができる

対数には以下のような便利な性質があります。

log(a×b) = log(a) + log(b)

log(a/b) = log(a) – log(b)

log(aⁿ) = n * log(a)

対数の活用事例

大規模な計算の簡略化

123456　×　789012　はいくつ？概算※でも構わない。
概算でも電卓なしでは計算するにはかなり厳しいですが、「対数表」を使えば比較的簡単に概算できます
　(※正確な数字ではないが使用に耐えうるレベル)

手順は以下
１．問題は掛け算なので、なんとか足し算に変換することを考える
　→ x = 123456　×　789012

２．両辺を対数にする。ここで、基数が10の常用対数を取るのが一般的。(対数表に合わせる)
　　log₁₀X = log₁₀(123456×789012) = log₁₀123456 + log₁₀789012 と足し算に変形。

３．log₁₀123456は対数表にないのでさらに分解。
　　→123456 の桁数を考えると1.23456×10⁵ 。また掛け算が出てきたので足し算に直す
→log₁₀1.23456 + log₁₀10⁵ これは、log₁₀1.23456 + 5

４．対数表で、1.23を探す。0.0899。よって、log₁₀123456は、5.0899。

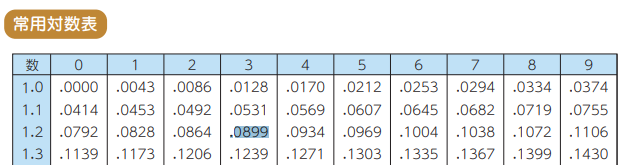
５．同様にすると、log₁₀789012は、5.8971。

６．求めたい式は以下なので、
　log₁₀X = log₁₀123456 + log₁₀789012 = 5.0899 + 5.8971 = 10.987

７．log₁₀X = 10.987 → X = 10^10.987 です。これが答えとしてもよいですが、まだよくわかりません。

10^10.987 = 10¹⁰ × 10^0.987 ここで10¹⁰はシンプルな数なので放っておくとして、問題は 10^0.987です。
　(0.987がほぼ1なので、10(=10¹ )よりちょっと少ない数字だな、と想像できますが)

８．ここで対数表を眺めます。0.987に近い数字がないか？と。ありました。
　log₁₀9.7 =0.9868だそうです。0.987 ≒ 0.9868 と考えると、 10^0.987　= 9.7です。

１０．答えは、およそ9.7 × 10¹⁰ となります。

 ８．で対数表から逆算する際に混乱することが多いと思います。
基本に戻り、対数表は「10の〇▼乗が0.9868」を示していることをしっかり気に留めておいてください。

日常や科学技術の中の対数

リヒタースケール（地震の強さ）

地震のマグニチュードは、地震が放出するエネルギーに大きく影響します。
その関係は次のような式で近似できます。
　E ∝ 10^1.5M
　E：地震が放出するエネルギー(J)
　M：マグニチュード

マグニチュードが1変わった場合(6から7)を想定すると、32倍もエネルギーが変わります。
　E₆ = k * 10^1.5*6 　= k * 10⁹
　E₇ = k * 10^1.5*7 　= k * 10^10.5
　E_7/E₆ = 10^1.5 ≒ 32 　(←計算は頑張ってください。10^0.5の処理がキモです)

1つの変数がわずかに変化しただけで、もう一つが爆発的に変化するような場合、対数で表現する方が都合がよいです

音の大きさ（デシベル）

デシベル（dB）も対数を用いて計算されます。これにより、音の強さを相対的に測りやすくなっています。

データ分析やAI

対数は、データの分布が広範囲にわたるとき、データを「圧縮」して見やすくするために使われます。
たとえば、収入分布のグラフを対数スケールにすることで、全体の傾向が分かりやすくなります。

まとめ

対数は、大規模な計算や指数的な変化を扱う際に非常に便利なツールです。
数学は過去の偉人たちが考えた便利ツールを教わる時間と考えてください。
今の時代電卓があるんだから不要だよね、と考えずぜひ学んでみてください！