楕円の魅力を解明：数学的特性と自然界での具体的な応用

はじめに

楕円と聞いて、どのようなイメージを抱きますか？「つぶれた円」程度の印象しかないのではないでしょうか？
しかし、楕円は数学的な美しさや自然界での重要性に満ちた図形です。この記事では、楕円の基本的な特徴から、その面白さや応用例まで掘り下げます。

楕円とは？

楕円とは、2つの焦点(点F、点F’)と呼ばれる特定の点からの距離の和が一定となる点Pの集合で形成される曲線です。
自分で作図するとよくわかります。一本の糸の両端を2点箇所(点F、点F’)に固定し、ぴんと張った状態でぐるっと回すと下記のような楕円を描くことができます。

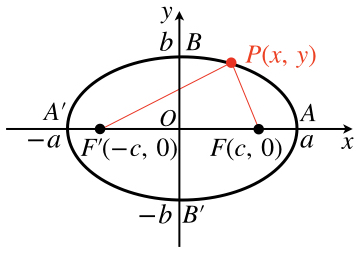
楕円の基本

数学的な楕円の性質の性質を示します。

各種式

楕円の形はこのシンプルな式で表現することができます。
　x²/a² + y²/b² = 1
　a ：　長軸半径
　b ：　短軸半径

面積もシンプルです。
　S = π × a × b
この式は円の面積=π × r² の単純な変形です。

ただ、周長だけは難しいです。正確な周長を求めるには楕円積分が必要です。
　C ＝4 × a ×　E(e)
　E(e) ： 楕円積分
　e ： 離心率　e = (1 – b²/a²)^1/2
積分なんて難しいのでラーマヌジャンの近似式を使います
　C ≒ π × (3×(a + b) – ( (3a + b)×(a +3b) )^1/2)

楕円の性質

楕円には次のような特性があります。

一方の焦点で発せられた波(音や光など)は楕円の周壁で反射すると、もう一方の焦点に集中する特性があります。

日常の中の楕円

・惑星の軌道
　楕円の応用で最も有名なものの一つが、ケプラーの惑星運動法則(第1法則)です。
　「惑星は太陽を焦点の1つとする楕円軌道を描く」
　宇宙規模の動きがこのシンプルな形に基づいていることは驚きです。

・セントポール大聖堂のささやきの回廊
　イギリスロンドンにあるセントポール大聖堂には「ささやきの回廊」という場所があります。
　小さい声で話しても30メートル以上離れた場所でもはっきりと声が聞こえるという不思議な体験ができます。
　これは楕円の特性を利用し、壁や天井に当たった反射波が一定の場所に集中するように設計されている為です。

まとめ

楕円は、数学的な抽象概念から自然界の現象、さらに日常の応用まで、多岐にわたる魅力を持っています。そのシンプルな形の中に潜む奥深い性質や、宇宙規模から人間の生活に至るまでの広範な影響をぜひ楽しんでみてください！